Lorenz gauge condition
In electromagnetism, the Lorenz gauge or Lorenz gauge condition is a partial gauge fixing of the electromagnetic vector potential. The condition is that 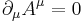 . This does not completely fix the gauge: one can still make a gauge transformation
. This does not completely fix the gauge: one can still make a gauge transformation 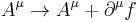 where
where  is a harmonic scalar function (that is, a scalar function satisfying
is a harmonic scalar function (that is, a scalar function satisfying 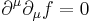 , the equation of a massless scalar field).
, the equation of a massless scalar field).
The Lorenz condition is used to eliminate the redundant spin-0 component in the (1/2,1/2) representation of the Lorentz group. It is equally used for massive spin-1 fields where the concept of gauge transformations does not apply at all.
The Lorenz condition is named after Ludvig Lorenz. It is a Lorentz invariant condition, and is frequently called the "Lorentz condition" because of confusion with Hendrik Lorentz, after whom Lorentz covariance is named.
Contents |
Description
In electromagnetism, the Lorenz condition is generally used in calculations of time-dependent electromagnetic fields through retarded potentials.[1] The condition is
where  is the four-potential, the comma denotes a partial differentiation and the repeated index indicates that the Einstein summation convention is being used. The condition has the advantage of being Lorentz invariant. It still leaves substantial gauge degrees of freedom.
is the four-potential, the comma denotes a partial differentiation and the repeated index indicates that the Einstein summation convention is being used. The condition has the advantage of being Lorentz invariant. It still leaves substantial gauge degrees of freedom.
In ordinary vector notation and SI units, the condition is:
where A is the magnetic vector potential and 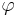 is the electric potential; see also Gauge fixing.
is the electric potential; see also Gauge fixing.
In Gaussian units the condition is:
It can be shown that with this gauge the physical information in the inhomogeneous part of Maxwell's equations can be expressed in the operationally simpler and symmetric form:
Here 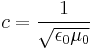 is the vacuum velocity of light, and
is the vacuum velocity of light, and  is the d'Alembertian operator. Interestingly, and unexpectedly at a first glance, these equations are not only valid under vacuum conditions, but also in polarized media [2] , if
is the d'Alembertian operator. Interestingly, and unexpectedly at a first glance, these equations are not only valid under vacuum conditions, but also in polarized media [2] , if  and
and 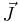 are source density and circulation density, respectively, of the electromagnetic induction fields
are source density and circulation density, respectively, of the electromagnetic induction fields 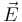 and
and 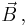 calculated as usual from
calculated as usual from 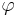 and
and 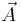 by the equations
by the equations 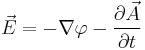 and
and  The explicit solutions for
The explicit solutions for 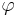 and
and 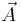 - unique, if all quantities vanish sufficiently fast at infinity - are known as retarded potentials.
- unique, if all quantities vanish sufficiently fast at infinity - are known as retarded potentials.
History
When originally published, Lorenz's work was not received well by James Clerk Maxwell. Maxwell had eliminated the Coulomb electrostatic force from his derivation of the electromagnetic wave equation since he was working in what would nowadays be termed the Coulomb gauge. The Lorenz gauge hence contradicted Maxwell's original derivation of the EM wave equation by introducing a retardation effect to the Coulomb force and bringing it inside the EM wave equation alongside the time varying electric field. Lorenz's work was the first symmetrizing shortening of Maxwell's equations after Maxwell himself published his 1865 paper. In 1888, retarded potentials came into general use after Heinrich Rudolf Hertz's experiments on electromagnetic waves. In 1895, a further boost to the theory of retarded potentials came after J. J. Thomson's interpretation of data for electrons (after which investigation into electrical phenomena changed from time-dependent electric charge and electric current distributions over to moving point charges).[1]
See also
References
- ^ a b McDonald, Kirk T. (1997), "The relation between expressions for time-dependent electromagnetic fields given by Jefimenko and by Panofsky and Phillips", American Journal of Physics 65 (11): 1074–1076, Bibcode 1997AmJPh..65.1074M, doi:10.1119/1.18723 and "pdf link". http://www.hep.princeton.edu/~mcdonald/papers/mcdonald_ajp_65_1176_97.pdf. Retrieved 1 June 2010..
- ^ See for example U. Krey, A. Owen, Basic Theoretical Physics - A Concise Overview, Berlin-Heidelberg-New York, Springer 2007.
External articles, and further reading
- General
- Eric W. Weisstein, "Lorenz Gauge".
- Further reading
- L. Lorenz, "On the Identity of the Vibrations of Light with Electrical Currents" Philos. Mag. 34, 287-301, 1867.
- J. van Bladel, "Lorenz or Lorentz?". IEEE Antennas Prop. Mag. 33, 2, p. 69, April 1991.
- R. Becker, "Electromagnetic Fields and Interactions", chap. DIII. Dover Publications, New York, 1982.
- A. O'Rahilly, "Electromagnetics", chap. VI. Longmans, Green and Co, New York, 1938.
- History
- R. Nevels, C.-S. Shin, "Lorenz, Lorentz, and the gauge", IEEE Antennas Prop. Mag. 43, 3, pp. 70–1, 2001.
- E. Whittaker, "A History of the Theories of Aether and Electricity", Vols. 1-2. New York: Dover, p. 268, 1989.
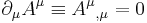
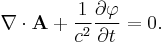
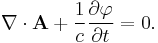
![\Box \vec{A}=\left[\frac{1}{c^2}\frac{\partial^2}{\partial t^2}-\nabla^{2}\right]\vec{A} = \mu_0\vec{J}](/2012-wikipedia_en_all_nopic_01_2012/I/b75a059c8778280373475e905afbe7d6.png)
![\Box\varphi = \left[\frac{1}{c^2}\frac{\partial^2}{\partial t^2} - \nabla^{2}\right] \varphi = \frac{1}{\epsilon_0}\rho\,.](/2012-wikipedia_en_all_nopic_01_2012/I/af61cd406eb954e0c59f474013214124.png)